Commutative Law of Addition

TOPIC OVERVIEW

In this article, I will explain the use of the Commutative Law of Addition, and suggest a better way of thinking about the topic. Please add your ideas in the comments.

THE COMMUTATIVE LAW

("change" the order of the numbers or letters)

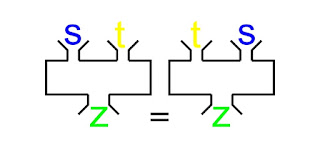
Over the years, people have found that when we add or multiply, the order of the numbers will not affect the outcome. "Switching" or "changing" the order of numbers is called "commuting". When we change the order of the numbers, we have applied the "Commutative Law". In an addition problem, it is referred to as the "Commutative Law of Addition" such that Addition on the Real Number ( 2, -5, and $ \frac{2}{7} $ )  S, T it is true  that   S+T = T+S

THE SUM OF 2 REAL NUMBERS

Example

Real Numbers 2 & 3

Let make S=2 & T=3

Solution

S+T = T + S

2+3 = 3 + 2

5 = 5

Note: - This is the sum of 2 positive real numbers. 

So let check if this is true for one positive and one negative number.

Example 2

Real numbers – 2 &3

Let S = -2, T= 3

Solution

S + T = T+ S

-2 + 3 = 3 + (-2)

1 = 3-2

1 = 1

Let try the result for 2 Negative Real Numbers

Example 3

Real Numbers – 3 & -1

Let S = -3, T = -1

Solution

S + T = T +S

-3 + (-1) = - 1 + (-3)

-3-1 = 1-3

-4= -4

The Commutative Law does not work for subtraction.
The order of the numbers will affect the outcome.

When you write 100 - 25, it is very different from 25 - 100.

The first case could be likened to writing a #25 check when you have #100 in the bank.
The other case, 25 - 100, would be an example of writing a #100 check when you have #25 in
the bank. Oops.....

One must be cautious with subtraction. If we look at the operation of subtraction as "adding the
opposite" then there may be a way to "commute" the numbers but in terms of addition and not
subtraction.

5 - 1 is not the same as 1 - 5.

The first case produces positive 4, but the second case yields negative 4.
We cannot commute the numbers in subtraction.

Yet, if we think of 5 - 1 as 5 + (-1), five plus the opposite of one, then the operation has been
changed from subtraction to addition. And we can commute in addition.

5 + (-1) is the same as (-1) + 5. Both "additions" will produce the number positive 4.

THE SUM OF 3 REAL NUMBERS

Let try the sum for any 3 Real Numbers a, b & c

a + b + c = b + a + c = c + a + b = a + c + b = b + c + a = c + b + a

We have 6 arrangements for the sum of 3 Real Numbers for each of our Example, we will be using 3 arrangements only you can work out the remaining 3.

Example

2 positive 1 Negative

Real Numbers 2, 1 & -3

Let a = 2, b = 1 c= -3

Solution

a + b + c = b + c + a = c + b + a

2 +1 +(-3) = 1 +(-3) +2 = -3 +1 +2

2 +1 -3 = 1 -2 +2 = -3 + 1 +2

3-3 = -2+2 = -2+2

0 =   0 = 0

Example 2

1 positive 2 Negative

Real Numbers 6, -2 & -1

Let a = 6, b = -2 & c = 1

Solution

a + b + c = b + c + a = c + b + a

6 +(-2) +(-1) = -2 +(-1) +6= -1 +(-2) +6

6-2-1= -2-1+6 = -1-2+6

4-1 = -3+6 = -3+6

3 = 3 =3

Example 3

Sum of Negative Numbers

Let a= -1, b= -2 & c = -4

Solution

a + c + b = b + a + c = c + a + b

-1 +(-2) + (-3) = -2 +(-1) +(-3) = -3 +(-1) +(-2)

-1 -2 -3 = -2 -1 -3 = -3 -1 -2

-3-3 = -3-1 = 4-2

-6 = -6 = -6

KEY IDEA:

We commute when we add, but we cannot commute or "change" the order of the
numbers when we subtract. So (3 + 4) + 10 will give you the same answer as (4 + 3 ) +
10 because we used the Commutative Law of Addition.

Question for try 

1.      9 - 2 - 5

2.      2 + 3 + 4

3.      3 - 2 + 4

4.      2 + 1 – 8

5.      -7 + 2 - 1

Use Commutative Law of Addition to solve your Addition and Subtraction problems it helps you understand the Relationship between Real Number.